O que é plano cartesiano?

O que é plano cartesiano? Trata-se de um plano constituído por duas retas numéricas perpendiculares nas quais é possível marcar localizações.

O plano cartesiano é um objeto matemático plano e composto por duas retas numéricas perpendiculares, ou seja, retas que possuem apenas um ponto em comum, formando um ângulo de 90°. Esse ponto comum é conhecido como origem e é nele que é marcado o número zero de ambas as retas. O plano cartesiano recebeu esse nome por ter sido idealizado por René Descartes e é usado fundamentalmente para sistematizar técnicas de localização no plano Retas numéricas: abcissa e ordenada


As duas retas que dão origem ao plano cartesiano precisam ser retas numéricas, pois essa é a condição que tornará possível encontrar localizações de pontos quaisquer no plano. Essa localização é a base fundamental de muitos conhecimentos comuns no cotidiano, como distância entre pontos.



Uma reta numérica é uma reta comum em que foi estabelecida uma correspondência com os números reais. Desse modo, cada ponto da reta está ligado a um único número real e é esse fato que permite qualquer localização. Um número real qualquer terá apenas uma localização em toda a extensão infinita da reta.

O plano cartesiano é formado por duas dessas retas: Uma responsável pela coordenada horizontal e outra responsável pela coordenada vertical. É comum usar as letras x para a primeira e y para a segunda e os termos “coordenada x” e “coordenada y”.


No plano cartesiano, a reta vertical responsável pelas coordenadas y é chamada de ordenada, e a reta horizontal, responsável pelas coordenadas x, é chamada de abcissa.

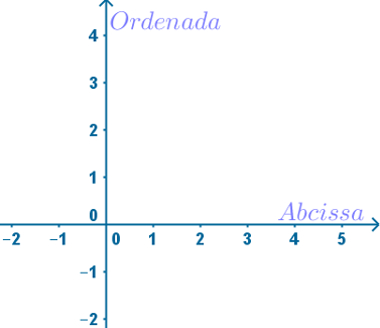
Plano cartesiano com destaque para a abcissa e a ordenada


Pares ordenados e localizações no plano


Um par ordenado é formado por dois números reais que representam uma coordenada. A ordem escolhida é a seguinte: Primeiro vêm as coordenadas x e, depois, as coordenadas y, que são colocadas entre parênteses para representar uma localização qualquer. Por exemplo, observe a imagem a seguir:

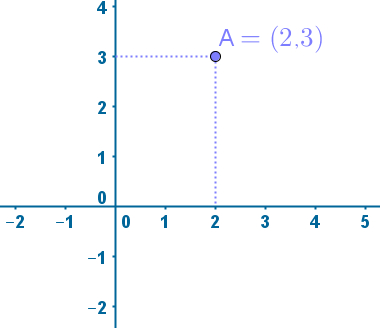
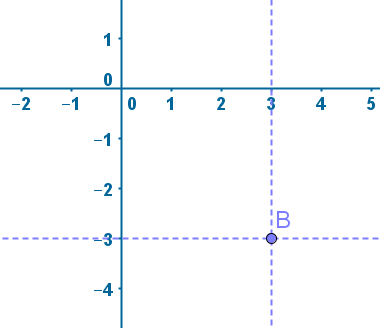
Perceba que o ponto A possui coordenadas x = 2 e y = 3. Caso seja dado um ponto para que sua localização seja marcada no plano, como o ponto B = (3, -3), devemos primeiro traçar uma linha vertical sobre o número 3 no eixo das abcissas (coordenadas x). Isso acontece porque a primeira coordenada sempre é a coordenada x. Posteriormente, desenhamos uma linha horizontal sobre o número – 3 no eixo das ordenadas (coordenadas y):

O ponto B é o encontro entre as linhas horizontais desenhadas, como ilustra a imagem acima.


Quadrantes


Por ser formado por duas retas numéricas, existem algumas particularidades do plano cartesiano. Pontos mais à direita possuem coordenada x maior que pontos mais à esquerda. Pontos mais para cima possuem coordenada y maior que números mais para baixo.


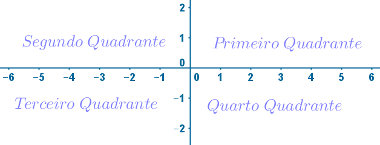
Além disso, a região onde x e y são positivos simultaneamente é chamada de primeiro quadrante. A região onde y é positivo e x é negativo é conhecida como segundo quadrante. Já a região onde x e y são negativos simultaneamente é chamada de terceiro quadrante. Por fim, quando x é positivo e y é negativo, os pontos estão localizados no quarto quadrante.


Esses quadrantes são numerados em sentido anti-horário, partindo do primeiro quadrante, que fica à direta do eixo y e acima do eixo x, como mostra a figura a seguir:

O que é fração?

Fração é uma palavra que vem do latim "fractus" e significa "partido", "quebrado", assim podemos dizer que fração é a representação das partes iguais de um todo.Veja o exemplo abaixo e perceba como identificar e utilizar uma fração.

Em uma lanchonete é vendido pedaços de pizza. A pizza inteira tem 6 pedaços iguais e custa R$ 9,00. Para que o dono dessa lanchonete descubra qual o valor que será arrecadado com cada pedaço vendido é preciso que conheça um pouco sobre fração, veja porque:

Se a pizza inteira foi dividida em 6 partes iguais e não foi vendido nenhum pedaço, podemos fazer a representação dessa divisão em forma de fração: . Isso significa que dos seis pedaços que a pizza foi dividida ainda há os 6.

A partir do momento que for vendida qualquer quantidade, por exemplo 2 pedaços, a representação irá mudar, então a fração que irá representar a parte que foi vendida é , ou seja, dos 6 pedaços foram vendidos 2, e a representação das partes que sobraram da pizza será 4, ou seja de 6 pedaços que a pizza possuía ainda não foram vendidos.
Conforme o que foi dito acima, representa o número de pedaços vendidos, para 

descobrir por quanto sai cada pedaço vendido o dono da lanchonete deve dividir o valor total da pizza pela quantidade de pedaços que ela foi repartida:

9 : 6 = 1,50, agora multiplicamos o valor de cada pedaço (R$1,50) pela quantidade de pedaços vendidos.
Portanto, como foi vendido apenas da pizza dizemos que foi arrecadado apenas R$3,00.

O que é uma função?

Função é uma regra que relaciona cada elemento de um conjunto (representado pela variável x) a um único elemento de outro conjunto (representado pela variável y). Para cada valor de x, podemos determinar um valor de y, dizemos então que “y está em função de x”.
Vamos representar uma função de números naturais de forma que, para cada número natural escolhido, obtenha-se o seu dobro. Por exemplo, se escolhermos o 1, teremos o número 2; se escolhermos o 2, teremos o 4; se escolhermos o 3, teremos o 6 e assim por diante. Podemos representar uma função utilizando o diagrama de flechas ou o diagrama de setas, como na figura a seguir:

O que é trigonometria?

Trigonometria é uma palavra de origem grega que remete à medida de três ângulos. Os estudos dessa área da Matemática voltam-se para os triângulos, que são polígonos que possuem três lados e, consequentemente, três ângulos. Em um primeiro momento, a trigonometria ocupa-se de estudar algumas propriedades e relações dos triângulos retângulos para posteriormente relacionar as medidas dos lados dos triângulos com as medidas dos ângulos.

O que é Matemática?

ciência que estuda, por método dedutivo, objetos abstratos (números, figuras, funções) e as relações existentes entre eles.